Introducing, the
Cartesian Plane

Picture a quiet evening in the 1600s, with the great philosopher René Descartes lying in bed, deep in thought. As he stared up at the ceiling, a small fly caught his attention, darting randomly across the room. But to Descartes, it wasn’t just a fly—it was a puzzle.

How could he describe the fly’s exact position, especially as it moved? Inspiration struck as he imagined the ceiling divided into tiles, like a giant grid. By counting tiles from one edge and then from another, he realized he could pinpoint the fly’s position with just two numbers. This idea was revolutionary, forming the basis of what we now call the Cartesian Plane.

What began as a simple observation would go on to change mathematics, giving us a powerful tool to map the world in numbers.

The Cartesian Plane

The Cartesian plane, also known as the coordinate plane, is a two-dimensional plane formed by the intersection of a horizontal number line called the x-axis and a vertical number line called the y-axis.

tldr: The Cartesian plane is a two-dimensional plane used to locate points.

Its components include:

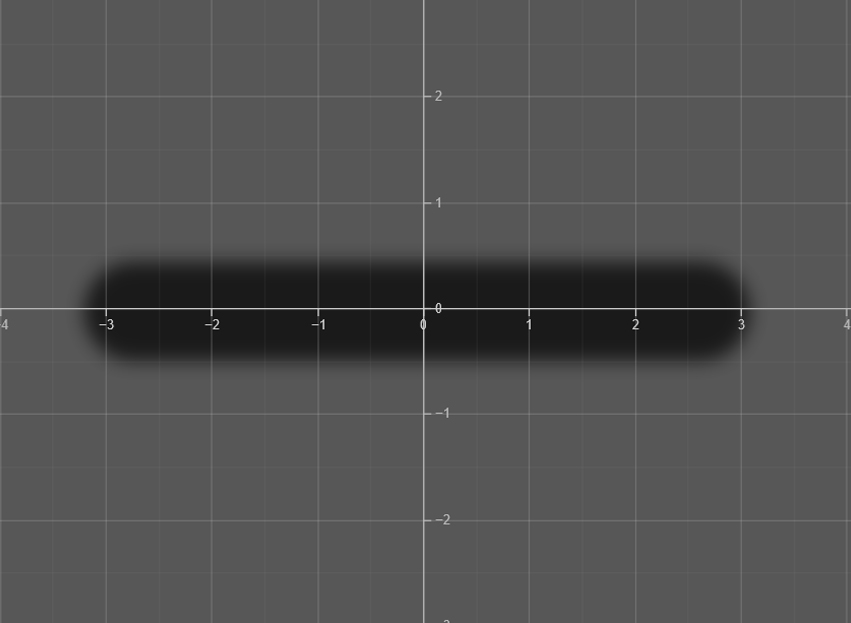
The x-axis

The x-axis is the horizontal line in the Cartesian plane where points are plotted from left to right.

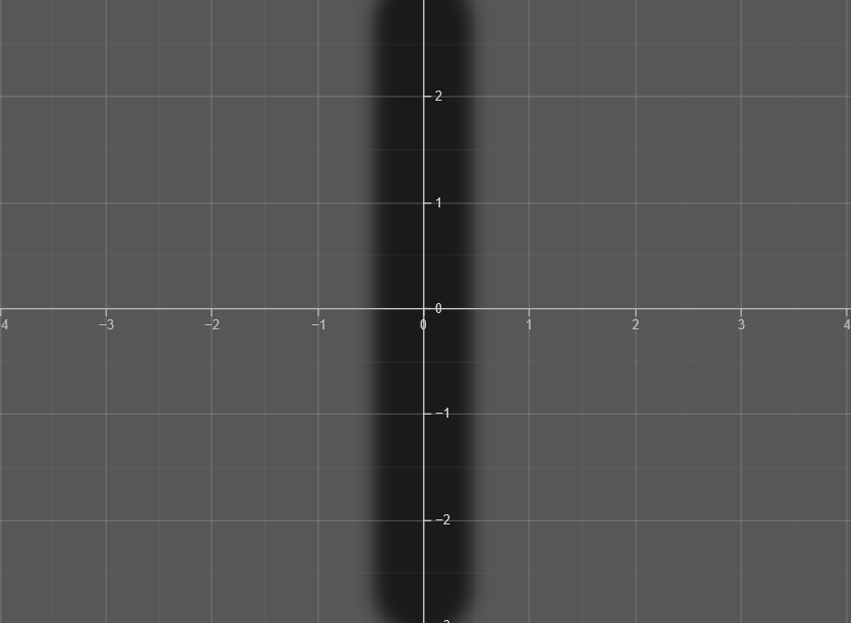
The Y Axis

The y-axis is the vertical line in the Cartesian plane where points are plotted from bottom to top.

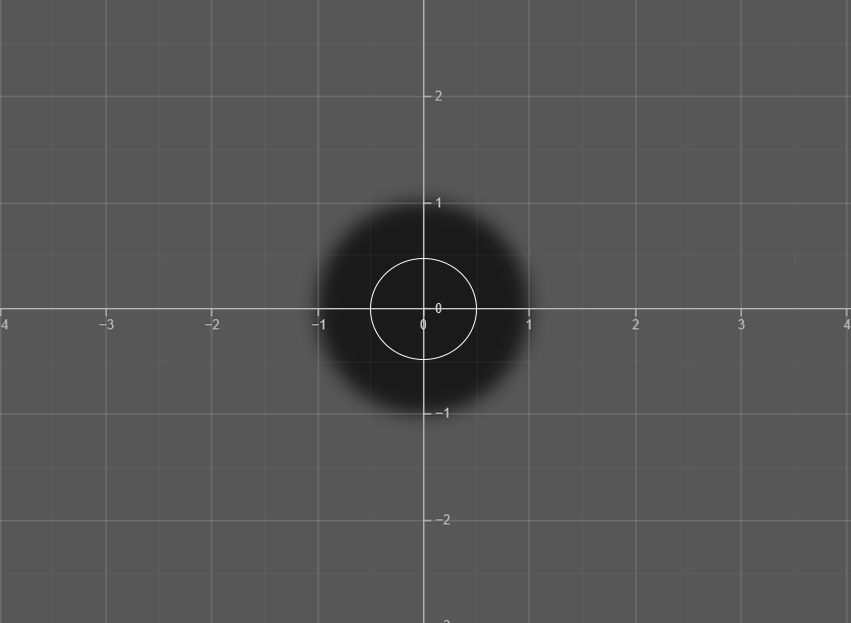
The Origin

The origin is the point where the x-axis and y-axis intersect, with coordinates (0, 0).

The Quadrants

The Cartesian plane is divided into four sections called quadrants, numbered counterclockwise from the top right.

Plotting Points

Points are plotted using a pair of numbers called coordinates (x, y). Here:

• x denotes the position from the origin, left or right.
• y denotes the position from the origin, bottom or top.

Steps to plot points:

1. Locate the origin.
2. Move x units left or right from the origin.
3. Move y units top or bottom from the origin.
4. Plot the point where the two lines intersect.

For example, plotting (3, 4):

1. Locate the origin.
2. Move 3 units right.
3. Move 4 units up.
4. Plot the point at (3, 4).

Try plotting the point (2, 2).

Determining the Position of a Point

A point’s position on the Cartesian plane is determined by its coordinates.

Steps:

1. Locate the origin.
2. Count units from the origin to the left or right.
3. Count units from the origin to the top or bottom.
4. Write the point’s coordinates.

For example, determining the position of Point A:

1. Locate the origin.
2. Count 3 units right.
3. Count 4 units up.

Thus, Point A is at (3, 4).

Try determining the position of Point B.

Quadrants

The Cartesian plane has four sections called quadrants, numbered counterclockwise from the top right.

Quadrants:

1. Quadrant I: Top right, where x and y are positive.
2. Quadrant II: Top left, where x is negative, y is positive.
3. Quadrant III: Bottom left, where x and y are negative.
4. Quadrant IV: Bottom right, where x is positive, y is negative.

Now, try identifying the quadrants for different points.

Great! You’ve now learned to plot points, determine a point’s position, and identify quadrants. You’re ready to explore more about the Cartesian plane!

Need a video explanation?